从一道有关欧拉函数的题目说起
今天从一个群里看到有人给了 Project Euler 上的第 69 题,并且说自己的算法跑了 40 分钟才算出来,说得我很好奇这到底是一个什么样的题。
我们来看题目:
Euler’s Totient function, φ(n) [sometimes called the phi function], is used to determine the number of numbers less than n which are relatively prime to n. For example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, φ(9)=6.
| n | Relatively Prime | φ(n) | n/φ(n) |
|---|---|---|---|
| 2 | 1 | 1 | 2 |
| 3 | 1,2 | 2 | 1.5 |
| 4 | 1,3 | 2 | 2 |
| 5 | 1,2,3,4 | 4 | 1.25 |
| 6 | 1,5 | 2 | 3 |
| 7 | 1,2,3,4,5,6 | 6 | 1.1666… |
| 8 | 1,3,5,7 | 4 | 2 |
| 9 | 1,2,4,5,7,8 | 6 | 1.5 |
| 10 | 1,3,7,9 | 4 | 2.5 |
It can be seen that n=6 produces a maximum n/φ(n) for n ≤ 10.
Find the value of n ≤ 1,000,000 for which n/φ(n) is a maximum.
题目读起来倒是没什么难度。但如果完全暴力求解的话,估计就得跑 40 分钟了,我们需要更优雅的做法。
看了题目后,直觉告诉我答案应该是把质数从小的一路乘上来(如 2 * 3 * 5…),得到比题目要求的 1,000,000 小的最大值就可以了。
于是给出了如下做法
1 | // 待补充 |
得到的答案是 510510,尝试提交,成功!
(其实就是从 2 乘到 17 就可以了完全不用写代码啊喂!)
这时候我们再回过来头看看这个思路。
题目要求 n/φ(n) 的最大值。
那么,只要尽量让 φ(n) 小,同时让 n 尽量大就可以了。
那么,就是尽量让 n 更多地与比它小的数有公约数。
那么,干脆让 n 由比它小的质数(从小到大,因为公约数 2 能覆盖的数字比 7 多多了)乘起来就好了,这样就能覆盖更多的数字,同时不浪费 n 的大小。(因为把 2 乘两遍并没有什么用)
Ok,这个直觉确实是对的,所以如何从数学上证明呢。
只要翻看欧拉函数的 wiki 就能证明了。
根据 wiki 内推导,我们有: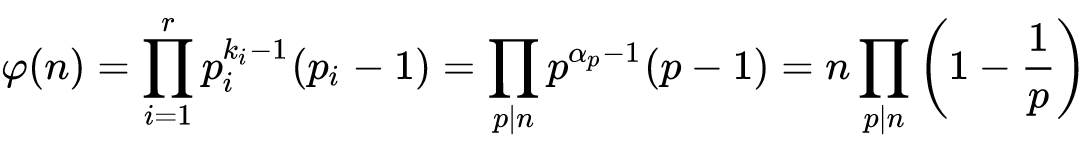
那么,题目最终要求解的即是: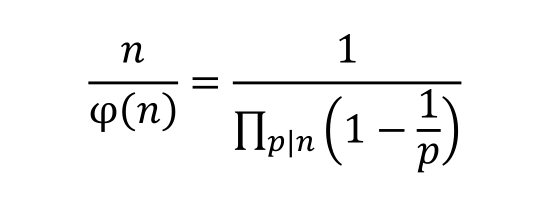
欲使上式右边最大,则使分母最小。
又因为分母里连乘的单项小于 1,则 p 越小越多即可。
故得 n 应从质数的最小值(2)一路乘上去。
所以答案为: 2 * 3 * 5 * 7 * 11 * 13 * 17 = 510510。
(为什么不再乘一个 19?你猜。)
(如果真的要再写公式的话,得考虑一下集成 LaTeX 了。)